Whether you’re counting pencils in your bag, scoring marks in a test, or solving algebraic equations, whole numbers form the foundation of mathematics. Understanding them clearly builds confidence for higher-level topics like integers, fractions, and algebra. This guide breaks down everything you need to know about whole numbers in the simplest way possible.
What is a Whole Number?
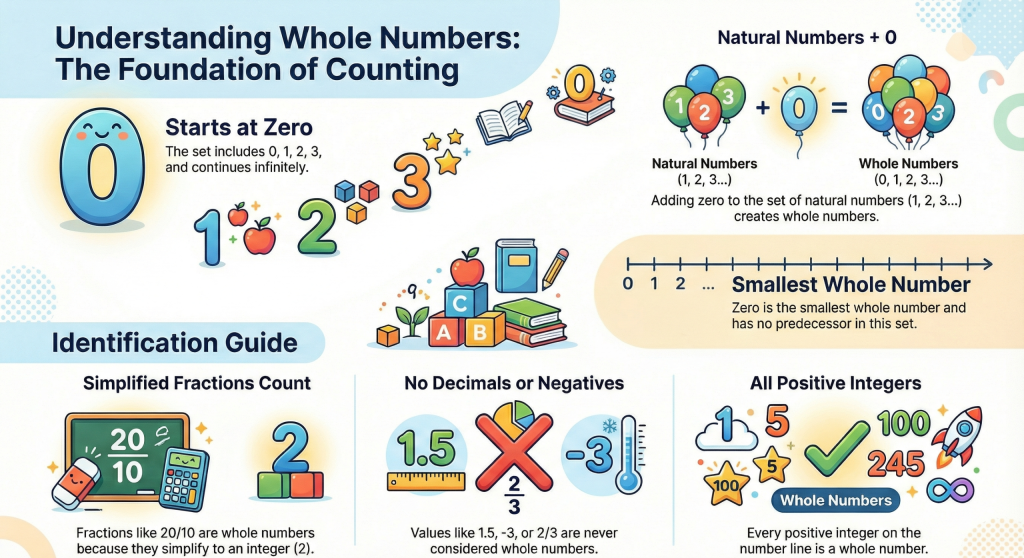
A whole number is any number that represents a complete quantity without fractions, decimals, or negative values.
Think of whole numbers as counting numbers that start from zero and go upward infinitely: 0, 1, 2, 3, 4, 5…
You use whole numbers every day:
- Counting books on a shelf
- Marking your attendance roll number
- Scoring runs in cricket
- Measuring the number of chapters in a textbook
Whole numbers are clean, simple, and always non-negative.
Whole Numbers Definition
Definition: Whole numbers are the set of numbers that include zero and all positive counting numbers (natural numbers) without any fractions or decimals.
Mathematical Representation:
W = {0, 1, 2, 3, 4, 5, 6, …}
Main Point:
- Start from 0
- Go infinitely in the positive direction
- No fractions (like 2.5) or decimals (like 3.14)
- No negative numbers (like -1, -5)
Is 0 a Whole Number?
Yes, 0 is a whole number.
This often confuses students because they associate counting with starting from 1. However, mathematically, zero represents “nothing” or “absence of quantity,” and it’s included in the set of whole numbers.
Example: If you have zero candies in your pocket, you’re stating a countable (though empty) quantity that’s a whole number.
Pro-Tip: Remember, natural numbers start from 1, but whole numbers start from 0. That’s the only difference between them.
Are All Natural Numbers Also Whole Numbers?
Yes, every natural number is a whole number.
Natural numbers are counting numbers: 1, 2, 3, 4, 5…
Whole numbers include all natural numbers plus zero: 0, 1, 2, 3, 4, 5…
Visual Breakdown:
| Natural Numbers | Whole Numbers |
|---|---|
| 1, 2, 3, 4, 5… | 0, 1, 2, 3, 4, 5… |
Since whole numbers simply add zero to the set of natural numbers, every natural number automatically qualifies as a whole number.
Properties of Whole Numbers
Whole numbers follow important mathematical properties that make calculations easier:
1. Closure Property
Adding or multiplying two whole numbers always gives a whole number.
- Example: 5 + 3 = 8 (whole number)
- Example: 4 × 2 = 8 (whole number)
2. Commutative Property
Order doesn’t matter in addition and multiplication.
- 7 + 2 = 2 + 7 = 9
- 3 × 5 = 5 × 3 = 15
3. Associative Property
Grouping doesn’t affect the result.
- (2 + 3) + 4 = 2 + (3 + 4) = 9
- (2 × 3) × 4 = 2 × (3 × 4) = 24
4. Additive Identity
Adding 0 to any whole number gives the same number.
- 8 + 0 = 8
5. Multiplicative Identity
Multiplying any whole number by 1 gives the same number.
- 9 × 1 = 9
Examples of Whole Numbers
Whole Numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11… and so on.
What are NOT whole numbers:
- Fractions: 1/2, 3/4
- Decimals: 2.5, 7.89
- Negative numbers: -1, -10, -50
Real-Life Examples:
- Number of students in your class: 40 (whole number)
- Your exam score: 85 (whole number)
- Pages in your textbook: 250 (whole number)
- Temperature in negatives: -5°C (NOT a whole number)
How Many Whole Numbers Are There Between 32 and 53?
To find whole numbers between two numbers, exclude the boundary numbers themselves.
Between 32 and 53:
33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52
Count: 20 whole numbers
Formula Shortcut:
Number of whole numbers between a and b = (b – a – 1)
= 53 – 32 – 1
= 20
Common Mistake: Students often include 32 and 53 in the count. Remember, “between” means excluding the endpoints.
Which is the Smallest Whole Number?
The smallest whole number is 0.
Whole numbers start from zero and continue infinitely: 0, 1, 2, 3…
Why not 1?
Because the set of whole numbers is defined to include zero.
Difference Between Whole Numbers and Integers
Students often confuse whole numbers with integers. Here’s the clear difference:
| Whole Numbers | Integers |
|---|---|
| 0, 1, 2, 3, 4… | …-3, -2, -1, 0, 1, 2, 3… |
| Only non-negative | Includes negative numbers |
| Starts from 0 | Extends in both directions |
Main Point: Every whole number is an integer, but not every integer is a whole number.
Example: -5 is an integer but NOT a whole number.
Common Mistakes Students Make
- Confusing Whole Numbers with Natural Numbers: Remember: Whole numbers include 0, natural numbers don’t.
- Thinking Negative Numbers are Whole Numbers: Whole numbers are always non-negative. -3, -10 are integers, not whole numbers.
- Including Fractions or Decimals: 2.5 and 1/2 are NOT whole numbers. Whole numbers must be complete without parts.
- Counting Endpoints When Finding “Between” Numbers: Between 10 and 20 means 11 to 19, not including 10 and 20.
Easy Tips to Remember Whole Numbers
Memory Trick: “Whole = Zero + Natural”
Whole numbers are just natural numbers (1, 2, 3…) with zero added at the start.
Visual Aid: Imagine a number line starting from 0 going right infinitely no negatives, no fractions.
Checklist for Whole Numbers:
- Is it 0 or positive?
- Is it a complete number (no decimals)?
- Is it a counting number?
If yes to all three, it’s a whole number.
Frequently Asked Questions about Whole Numbers
Q. What is the difference between whole numbers and counting numbers?
Counting numbers (natural numbers) start from 1, while whole numbers start from 0. Whole numbers = {0, 1, 2, 3…}, and counting numbers = {1, 2, 3…}. So, whole numbers include zero along with all counting numbers.
Q. Is every integer a whole number?
No, not every integer is a whole number. Integers include negative numbers like -1, -2, -3, which are not whole numbers. However, every whole number is an integer since whole numbers are part of the integer set.
Q. Can whole numbers be negative?
No, whole numbers cannot be negative. They include only zero and positive counting numbers. Negative numbers fall under integers but are excluded from the whole number set. For example, -7 is an integer, not a whole number.
Q. What is the largest whole number?
There is no largest whole number. Whole numbers extend infinitely in the positive direction: 0, 1, 2, 3, 4… and so on. No matter how large a number you think of, you can always add 1 to get a bigger whole number.
Q. Are decimals considered whole numbers?
No, decimals are not whole numbers. Whole numbers must be complete without fractional or decimal parts. For example, 3.5, 7.89, and 0.25 are not whole numbers. Only numbers like 0, 1, 2, 3 qualify as whole numbers.
Q. How many whole numbers are there from 1 to 100?
There are 100 whole numbers from 1 to 100 (inclusive). If you include 0, then there are 101 whole numbers from 0 to 100. Remember, whole numbers start at 0, so always check if the question includes zero.
Q. Is 0.5 a whole number?
No, 0.5 is not a whole number because it contains a decimal part. Whole numbers must be complete, non-fractional quantities. Only numbers like 0, 1, 2, 3 are whole numbers, not values with decimals or fractions like 0.5 or 1/2.
Q. Why is 0 included in whole numbers?
Zero is included in whole numbers because it represents the absence of quantity, which is still countable. Mathematically, adding zero to natural numbers creates the set of whole numbers, making calculations and number theory more complete and consistent.
Conclusion
Whole numbers are the simplest building blocks of mathematics, representing complete, countable quantities starting from zero. Whether you’re solving homework problems, counting objects, or preparing for exams, a strong grasp of whole numbers sets you up for success in algebra, geometry, and beyond.
Remember: every natural number is a whole number, zero is the smallest whole number, and no negatives or fractions are allowed. Practice identifying whole numbers in everyday situations, and you’ll find math becomes much more intuitive.

