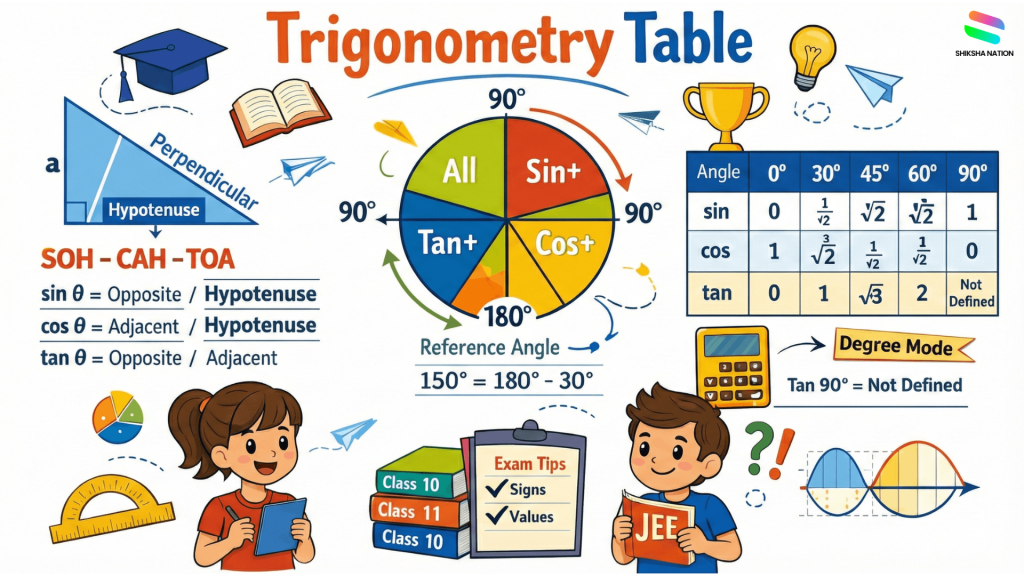
What Is a Trigonometry Table? (Concept Explained)
A trigonometry table is a structured chart that lists the values of basic trigonometric ratios for specific angles. It helps students quickly recall results without deriving them again and again during exams.
In a right-angled triangle, these ratios are formed using the sides of the triangle. These are called right angle triangle ratios. For any angle θ, the three main ratios are sine (sin), cosine (cos), and tangent (tan).
Understanding sin, cos and tan
Sin θ is the ratio of perpendicular to hypotenuse.
Cos θ is the ratio of base to hypotenuse.
Tan θ is the ratio of perpendicular to base.
Many students remember this using SOHCAHTOA, which makes learning easier and systematic. A trigonometry ratio table organizes these values clearly for standard angles.
The trigonometry table sin cos tan is very important for Class 10 board exams and JEE preparation. Questions on heights and distances, identities, and equations often depend directly on these values. Having clarity here saves time and reduces mistakes.
Standard Trigonometry Table (0°, 30°, 45°, 60°, 90°)
These five angles are called standard angles because they come from special right-angled triangles. In Class 10, most board questions are based on these values. So every student should remember this basic table clearly.
Below is the trigonometry table 0 to 90 degree used in schools:
| Angle (θ) |
0° |
30° |
45° |
60° |
90° |
| sin θ |
0 |
1/2 |
1/√2 |
√3/2 |
1 |
| cos θ |
1 |
√3/2 |
1/√2 |
1/2 |
0 |
| tan θ |
0 |
1/√3 |
1 |
√3 |
Not defined |
| cosec θ |
Not defined |
2 |
√2 |
2/√3 |
1 |
| sec θ |
1 |
2/√3 |
√2 |
2 |
Not defined |
| cot θ |
Not defined |
√3 |
1 |
1/√3 |
0 |
Trigonometry Table 0 to 90 Degree (Class 10 Focus)
In the class 10th trigonometry table, these angles are standard because they are derived from 30-60-90 and 45-45-90 triangles.
For example, sin 30 value is 1/2 and cos 60 value is also 1/2. This shows symmetry in the table.
Similarly, tan 45 value is 1 because perpendicular and base are equal in a 45° triangle.
Students must also remember undefined trigonometric values. Tan 90° is not defined because cos 90° is zero. Cot 0° is not defined for a similar reason.
This basic trig table class 10 forms the foundation of all higher concepts.
Full Trigonometry Table (0° to 360°)
For higher classes and competitive exams, students need the trigonometry table 0 to 360. Instead of memorising every value again, we use sign rules and logic.
Quadrant Sign Rule Explained Simply
A full circle is divided into four quadrants:
- 0°–90° → 1st quadrant
- 90°–180° → 2nd quadrant
- 180°–270° → 3rd quadrant
- 270°–360° → 4th quadrant
In the 1st quadrant, all ratios are positive.
In the 2nd quadrant, only sine is positive.
In the 3rd quadrant, only tangent is positive.
In the 4th quadrant, only cosine is positive.
This is called the quadrant sign rule.
Sin Cos Value Table 0 to 360 – How to Derive
To build the sin cos value table 0 to 360, we use the same standard values from 0°–90°. Then we apply the sign rule based on the quadrant.
For example, sin 150° = sin (180° – 30°). Here 30° is the reference angle concept. Since it lies in the 2nd quadrant, sine remains positive.
This method helps students understand the full trigonometry angle table without memorising long lists. It is especially useful for Class 11 and JEE preparation.
Full Trigonometry Table (0° to 360°)
In higher classes and competitive exams, students are expected to know the trigonometry table 0 to 360, not just the basic 0°–90° values. Many questions in Class 11 and JEE are based on angles like 120°, 225°, or 330°.
Instead of memorising a very long trigonometry angle table, it is better to understand the logic behind how values change in different parts of a circle. Once the concept is clear, students can confidently find any value without confusion.
Quadrant Sign Rule Explained Simply
A full circle is divided into four parts called quadrants.
0°-90° is the 1st quadrant.
90°-180° is the 2nd quadrant.
180°-270° is the 3rd quadrant.
270°-360° is the 4th quadrant.
According to the quadrant sign rule, all ratios are positive in the first quadrant.
In the second quadrant, only sine is positive.
In the third quadrant, only tangent is positive.
In the fourth quadrant, only cosine is positive.
This simple pattern helps students avoid sign mistakes in exams.
The reference angle concept means we take the related acute angle (between 0° and 90°) to find the value, then apply the correct sign based on the quadrant.
Sin Cos Value Table 0 to 360 – How to Derive
To create the sin cos value table 0 to 360, start with the standard values from 0° to 90°.
For example, to find sin 150°, we write it as sin (180° – 30°). Here, 30° is the reference angle. Since 150° lies in the second quadrant, sine remains positive.
Similarly, cos 210° can be written as cos (180° + 30°). The reference angle is again 30°, but cosine becomes negative in the third quadrant.
By using this method, students do not need to memorise a long sin cos value table 0 to 360. They only need the basic values and a clear understanding of sign rules.
This approach builds confidence and reduces errors in board and entrance exams.
Trigonometric Functions Table (Including Sec, Cosec, Cot)
In addition to sin, cos and tan, students must also understand secant (sec), cosecant (cosec) and cotangent (cot). A complete trigonometric functions table includes all six ratios.
These extra ratios are not new concepts. They are based on reciprocal identities (sec, cosec, cot), which means they are simply the inverse of the main three ratios.
Understanding Reciprocal Identities
Cosec θ = 1 / sin θ
Sec θ = 1 / cos θ
Cot θ = 1 / tan θ
So, if you already know the basic values from the full trigonometry table, you can easily find sec, cosec and cot by taking the reciprocal.
Students often get confused about undefined values. Sec 90° is undefined because sec θ = 1 / cos θ, and cos 90° equals 0. Division by zero is not possible, so the value does not exist.
Similarly, cosec 0° is undefined because sin 0° equals 0. When we take 1 / 0, the value becomes undefined.
Understanding this logic is very important for boards and entrance exams. It helps students avoid common calculation mistakes and builds stronger conceptual clarity.
How to Memorise the Trigonometry Table Easily
Many students try to memorise the trigonometry table values by rote learning. But understanding the pattern makes it much easier and long-lasting.
√n/2 Pattern for Sine Values
For angles 0°, 30°, 45°, 60°, and 90°, sine follows a simple pattern.
Write numbers 0, 1, 2, 3, 4. Take the square root of each number and divide by 2.
So,
sin 0° = √0/2
sin 30° = √1/2
sin 45° = √2/2
sin 60° = √3/2
sin 90° = √4/2
This logical pattern helps students remember values without stress.
Reverse Logic for Cos and Relation of Tan
Cosine follows the same pattern but in reverse order.
If sine goes from 0 to 1, cosine comes from 1 to 0.
For tangent, no separate pattern is needed.
tan θ = sin θ / cos θ.
When students understand this relation, they do not need extra tricks. Logic-based learning is more helpful, especially for JEE trigonometry preparation, where speed and accuracy both matter.
Strong clarity in these values also helps in chapters like heights and distances, where direct substitution of standard angles is common.
Parents can encourage regular short practice instead of last-minute memorising. Consistent revision builds confidence in exams.
Common Mistakes Students Make in Exams
Even when students know the formulas, small mistakes in trigonometry can reduce marks. Most errors happen due to carelessness, not lack of knowledge.
Mixing Sine and Cosine Order
Many students confuse the order of sine and cosine values, especially in the trigonometry table ncert.
They may write sin 30° as √3/2 instead of 1/2. This usually happens when revision is not done properly.
Forgetting Undefined Values
Students sometimes forget about undefined trigonometric values like tan 90° or cosec 0°.
Writing any number instead of stating “not defined” can lead to loss of marks in boards and competitive exams.
Degree vs Radian Mode Error
In calculators, the degree vs radian mode setting is very important.
If the mode is set to radian instead of degree, answers will be completely wrong even if the method is correct.
Applying Wrong Quadrant Sign
In higher classes, students often apply the wrong sign in different quadrants.
A small sign mistake can change the final answer.
Regular practice and careful checking can help avoid these common errors.
Trigonometry Table for Class 10, 11 and JEE
The use of the trigonometry table changes slightly as students move from boards to competitive exams. The depth of understanding increases with each class.
Class 10 (Boards)
For trigonometry table class 10, focus is mainly on standard angles from 0° to 90°.
Questions are directly based on NCERT examples and exercises.
Students should clearly remember basic values and identify undefined cases. Regular practice from textbook problems is enough to score well in board exams.
Parents can ensure that students revise the table weekly instead of only before exams.
Class 11 Basics
In trigonometry table class 11, the approach becomes more conceptual.
Students learn about trigonometric functions and their graphs.
Understanding signs in different quadrants and linking values to the unit circle becomes important. These class 11 trigonometry basics build the foundation for higher maths.
JEE Preparation
For JEE trigonometry preparation, students must confidently use values from 0° to 360°.
Speed matters, especially in MCQs.
Strong command over sign rules and quick recall of standard values helps save time and avoid silly mistakes in competitive exams.
Trigonometry Table PDF (Printable Format)
A trigonometry table PDF is helpful when students want a quick revision sheet. Instead of searching online again and again, they can keep a printed copy in their notebook or study area.
Before exams, especially boards or entrance tests, a single-page full trigonometry table makes revision faster. Students can glance at the values daily and improve memory naturally.
For parents, a printable format is useful to support regular practice at home. They can encourage short revision sessions without creating extra pressure.
A clear and neatly arranged PDF works as a ready reference during last-minute preparation and helps build confidence.
Download the PDF – Trigonometry Table (0° to 360°) – Class 10, 11 & JEE PDF
FAQs on Trigonometry Table
Q. What is the trigonometry table?
The trigonometry table is a ready reference chart that shows the exact values of sine, cosine and tangent for important angles. These trigonometry table values help students solve questions quickly in exams without recalculating ratios every time. It is mainly used in Class 10, Class 11 and competitive exams where speed and accuracy both matter.
Q. What are the values of sin 30, cos 60, tan 45?
The sin 30 value is 1/2.
The cos 60 value is also 1/2. The tan 45 value is 1 because in a 45° triangle, the perpendicular and base are equal. These standard values are very important for board exam questions.
Q. Why is tan 90° undefined?
Tan θ is equal to sin θ divided by cos θ.
At 90°, cos 90° becomes 0. Since division by zero is not possible, tan 90° is not defined. Students should clearly write “not defined” in exams instead of leaving it blank.
Q. How to remember trigonometry table fast?
Instead of memorising randomly, understand the pattern of sine values using √n/2 logic. Then reverse the order for cosine and use tan = sin/cos. Daily short revision works better than last-minute learning. Parents can encourage 5-minute practice sessions regularly.
Q. Is trigonometry table enough for Class 10 board?
For most board questions, knowing standard angles and applying them correctly is enough. However, students must also understand basic concepts and avoid sign or calculation mistakes. Clear understanding plus correct use of the table helps score better marks confidently.