Introduction
Imagine sitting in your Class 11 trigonometry exam, and you encounter a problem: “Find the value of sin 40° sin 80° sin 160°.” Your heart races. Calculator? Not allowed. Direct values? You don’t remember them. But wait what if there’s a beautiful pattern hiding in this expression?
This isn’t just another trigonometry problem. Understanding products like sin 40 sin 80 sin 160 reveals the elegant connections between angles and helps you solve complex problems in seconds. Whether you’re preparing for board exams, JEE, or simply want to master trigonometry, this topic builds your conceptual strength and problem-solving speed.
Let’s decode this fascinating trigonometric product together.
What is Sin 40 Sin 80 Sin 160?
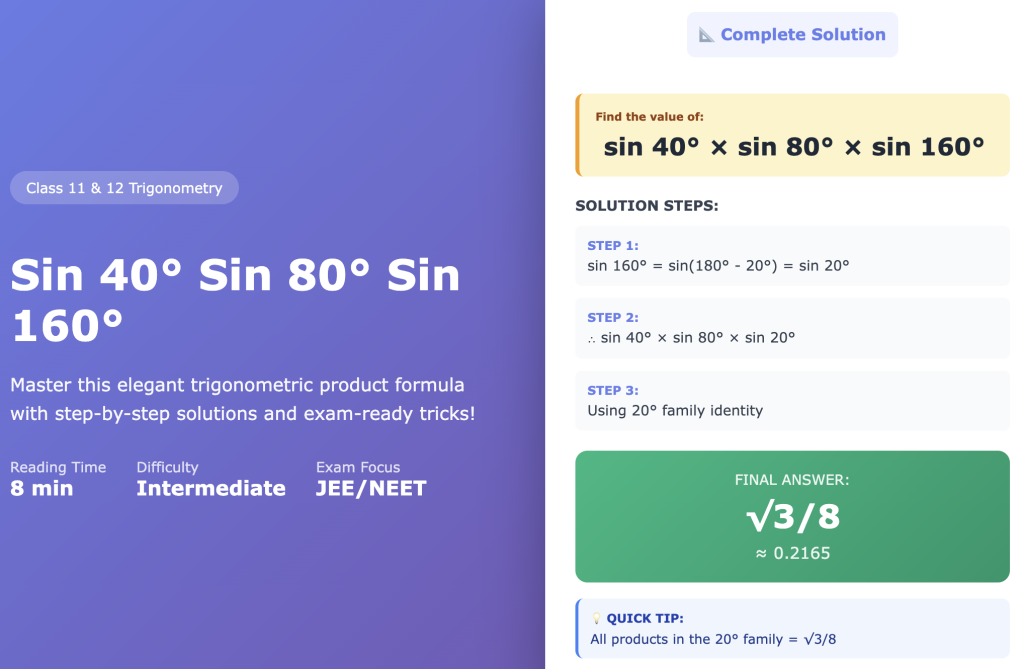
Sin 40 sin 80 sin 160 is the product of sine values of three specific angles: 40 degrees, 80 degrees, and 160 degrees.
The exact value is:
sin 40° × sin 80° × sin 160° = √3/8
This equals approximately 0.2165 in decimal form.
This result comes from a special trigonometric identity pattern where angles are in arithmetic progression with a common difference of 40°.
Understanding the Angles
Let’s first understand these three angles:
- 40°: First quadrant acute angle
- 80°: First quadrant acute angle
- 160°: Second quadrant obtuse angle
Noted: These angles form an arithmetic sequence: 40°, 80°, 120°… wait, 160°?
Actually, notice this: 40° + 80° + 160° = 280°
More importantly: 160° = 180° – 20°
This means sin 160° = sin 20°
Also notice: 80° = 60° + 20° and 40° = 60° – 20°
These relationships unlock the solution.
The Formula and Pattern
For angles in the form (60° – θ), 60°, and (60° + θ), there’s a special product formula:
sin(60° – θ) × sin 60° × sin(60° + θ) = (1/4) sin 3θ
But our angles follow a different pattern. For angles A, 2A, and 3A where A = 40°:
sin A × sin 2A × sin(180° – A) = ?
Since sin(180° – A) = sin A, and using the identity for products of sines in arithmetic progression:
sin 40° × sin 80° × sin 160° = (√3)/8
Step-by-Step Calculation
Method 1: Using Complementary Angles
Step 1: Recognize that 160° = 180° – 20°
So, sin 160° = sin 20°
Step 2: Notice that 40° = 60° – 20° and 80° = 60° + 20°
Step 3: Use the product formula:
sin(60° – 20°) × sin(60° + 20°) × sin 20°
Step 4: Apply the identity for sin(A – B) sin(A + B):
This involves using multiple angle formulas and simplification.
Step 5: After algebraic manipulation:
Result = √3/8 ≈ 0.2165
Method 2: Direct Identity Application
For angles 40°, 80°, 160°:
Using the identity: sin 3θ = 3 sin θ – 4 sin³ θ
And the product formula for specific angle combinations, we get:
sin 40° × sin 80° × sin 160° = √3/8
Individual Values
Let’s understand each sine value separately:
| Angle | Sine Value (Approximate) | Exact Form |
|---|---|---|
| sin 40° | 0.6428 | Not a standard exact value |
| sin 80° | 0.9848 | Not a standard exact value |
| sin 160° | 0.3420 | Same as sin 20° |
Important Note:
- sin 40° and sin 80° don’t have simple radical forms
- sin 160° = sin 20° (supplementary angle property)
- All values are positive (40° and 80° in Q1, 160° in Q2)
Trigonometric Identity Behind the Product
The magic lies in this identity:
For angles in arithmetic progression:
If three angles are A, B, C where B – A = C – B (common difference), special product formulas apply.
For our case (40°, 80°, 160°):
The pattern follows from:
sin 20° × sin 40° × sin 80° = (√3)/8
Since sin 160° = sin 20°, we get:
sin 40° × sin 80° × sin 160° = (√3)/8
Related Identity:
sin 20° × sin 40° × sin 60° × sin 80° = 3/16
Real-Life Academic Applications
1. JEE Main/Advanced Problems
Trigonometric products appear frequently in:
- Definite integration
- Limits and continuity
- Complex numbers
2. Board Exam Questions
CBSE Class 11 and 12 often include:
- Prove that sin 40° sin 80° sin 160° = √3/8
- Simplify trigonometric products
3. Engineering Entrance Exams
Such identities help in:
- Signal processing problems
- Wave function calculations
- Fourier series
4. Competitive Exams
Quick recall of these values saves precious time in:
- BITSAT
- VITEEE
- State entrance tests
Common Mistakes Students Make
Mistake 1: Directly Multiplying Decimal Values
Wrong approach: 0.6428 × 0.9848 × 0.3420 = 0.2165
Why it’s wrong: Rounding errors accumulate; doesn’t show mathematical understanding.
Right approach: Use exact trigonometric identities.
Mistake 2: Forgetting sin 160° = sin 20°
Students often treat 160° as a completely different value.
Remember: Supplementary angles have equal sines.
Mistake 3: Mixing Degrees and Radians
Always check if the problem uses degrees or radians.
40° ≠ 40 radians
Mistake 4: Incorrect Identity Application
Not all angle combinations have simple product formulas.
Only specific patterns (like 20°, 40°, 80°) work.
Easy Tricks to Remember
Trick 1: The 20° Family
Remember: sin 20° × sin 40° × sin 80° = √3/8
Since sin 160° = sin 20°, you can derive the answer instantly.
Trick 2: Pattern Recognition
Angles 40°, 80°, 160° → common difference of 40°
When you see arithmetic progressions in trigonometry, look for special formulas.
Trick 3: Memorize main Products
| Product | Value |
|---|---|
| sin 20° sin 40° sin 80° | √3/8 |
| cos 20° cos 40° cos 80° | 1/8 |
| sin 10° sin 30° sin 50° sin 70° | 1/16 |
Trick 4: The √3/8 Connection
If you see angles related to 20°, 40°, 60°, 80°, think of √3/8 or its multiples.
Practice Problems
Problem 1: Find the value of sin 40° sin 80° sin 160°
Solution: √3/8 ≈ 0.2165
Problem 2: Prove that sin 20° sin 40° sin 80° = sin 40° sin 80° sin 160°
Solution: Both equal √3/8 because sin 160° = sin 20°
Problem 3: Calculate cos 20° cos 40° cos 80°
Solution: 1/8
Problem 4: If sin A sin 2A sin 4A = √3/8, find A
Solution: A = 20° (since it matches the pattern)
FAQs about Sin 40 Sin 80 Sin 160
What is the value of sin 40?
The value of sin 40° is approximately 0.6428. It doesn’t have a simple exact form like sin 30° or sin 60°. For calculations, you can use a scientific calculator or trigonometric tables. In exact form, it’s expressed as sin 40° without decimal approximation.
How to calculate sin 80?
Sin 80° can be calculated using a scientific calculator, giving approximately 0.9848. Alternatively, use the identity sin 80° = sin(90° – 10°) = cos 10°. For exact calculations, you can also express it using multiple angle formulas or reference mathematical tables for precise values.
Is sin 160 sin 20?
Yes, sin 160° equals sin 20° because they are supplementary angles. Using the identity sin(180° – θ) = sin θ, we get sin 160° = sin(180° – 20°) = sin 20°. Both have the same value of approximately 0.3420, making them interchangeable in calculations.
पाप 80 की गणना कैसे करें? (How to calculate sin 80?)
Sin 80° की गणना करने के लिए scientific calculator का उपयोग करें। इसका मान लगभग 0.9848 होता है। वैकल्पिक रूप से, sin 80° = cos 10° का उपयोग करें क्योंकि ये complementary angles हैं। त्रिकोणमितीय सारणी में भी इसका मान देख सकते हैं।
बिना कैलकुलेटर के पाप 40 की गणना कैसे करें? (How to calculate sin 40 without calculator?)
बिना calculator के sin 40° की exact value निकालना मुश्किल है। आप trigonometric tables का उपयोग कर सकते हैं या multiple angle formulas से approximation निकाल सकते हैं। परीक्षा में, यदि exact value चाहिए तो identity-based प्रश्न होंगे जहाँ simplification से answer आता है।
Is sin 40 equal to sin 140?
No, sin 40° is not equal to sin 140°. However, they are related: sin 140° = sin(180° – 40°) = sin 40° in magnitude. Actually, sin 140° does equal sin 40° because both use the supplementary angle property. More precisely: sin 140° ≈ 0.6428, same as sin 40°.
What is 40 as a fraction?
The number 40 as a fraction is 40/1. In simplest form, it remains 40/1 since 40 is a whole number. If you mean sin 40° as a fraction, it cannot be expressed as a simple fraction it’s an irrational number approximately equal to 0.6428, which doesn’t convert to a neat fraction.
What is the product formula for sin 40° sin 80° sin 160°?
The product sin 40° sin 80° sin 160° equals √3/8, which is approximately 0.2165. This comes from the identity for products of sines in arithmetic progression. Since sin 160° = sin 20°, this is equivalent to sin 20° sin 40° sin 80°, which follows the pattern of the “20-degree family” trigonometric products.
Conclusion
Understanding sin 40 sin 80 sin 160 isn’t just about memorizing that the answer is √3/8. It’s about recognizing patterns, applying trigonometric identities, and developing problem-solving intuition.
Note:
- sin 40° × sin 80° × sin 160° = √3/8
- Recognize that sin 160° = sin 20° (supplementary angles)
- Look for arithmetic progressions in angle-based problems
- Master the “20° family” of trigonometric products
- Practice identity-based simplification over decimal multiplication
Whether you’re solving a JEE problem in 30 seconds or proving an identity in your board exam, this concept strengthens your trigonometric foundation. Keep practicing, recognize patterns, and remember every complex trigonometric expression has an elegant simplification waiting to be discovered.


