Understanding Variance in Statistics
Variance is a fundamental measure of dispersion in statistics that quantifies how far data points spread from their mean value. This guide provides all essential variance-related formulas with clear explanations for students at school and college levels.
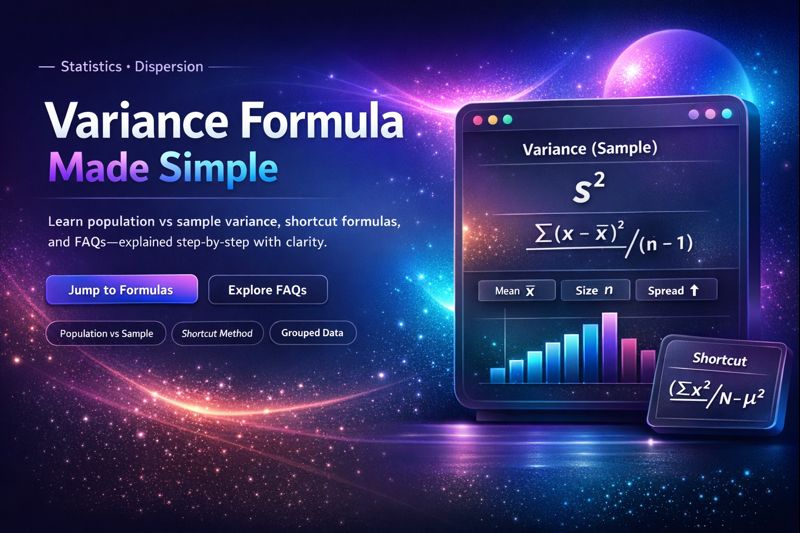
Complete Variance Formula
| Formula Name | Formula | When to Use | Explanation |
|---|---|---|---|
| Population Variance (σ²) | σ² = Σ(xᵢ – μ)² / N | When you have data for the entire population | Sum of squared deviations from population mean (μ) divided by total population size (N) |
| Sample Variance (s²) | s² = Σ(xᵢ – x̄)² / (n-1) | When you have a sample from a larger population | Sum of squared deviations from sample mean (x̄) divided by (n-1), where n is sample size. Uses (n-1) for unbiased estimation |
| Alternative Sample Variance | s² = [Σxᵢ² – (Σxᵢ)²/n] / (n-1) | Computational convenience with raw data | Algebraically equivalent to standard formula, often easier for calculations |
| Population Standard Deviation (σ) | σ = √[Σ(xᵢ – μ)² / N] | To express dispersion in original units (population) | Square root of population variance, returns to original measurement units |
| Sample Standard Deviation (s) | s = √[Σ(xᵢ – x̄)² / (n-1)] | To express dispersion in original units (sample) | Square root of sample variance, more interpretable than variance |
| Coefficient of Variation (CV) | CV = (σ/μ) × 100% or (s/x̄) × 100% | Comparing variability across different datasets or units | Expresses standard deviation as percentage of mean; useful for comparison |
| Variance of Grouped Data | σ² = Σf(xᵢ – μ)² / Σf | When data is organized in frequency distribution | Weighted variance where f is frequency of each class/value |
| Combined Variance (Two Groups) | σ² = [n₁σ₁² + n₂σ₂² + n₁(x̄₁-x̄)² + n₂(x̄₂-x̄)²] / (n₁+n₂) | Combining variances from two separate groups | Accounts for both within-group and between-group variation |
| Sxx Formula | Sxx = Σ(xᵢ – x̄)² = Σxᵢ² – (Σxᵢ)²/n | Calculating sum of squares for regression analysis | Sum of squared deviations; foundational for correlation and regression |
| Variance (Short-cut Method) | σ² = (Σxᵢ²/N) – μ² | Quick calculation with squared values | Mean of squares minus square of mean |
| Pooled Variance | s²ₚ = [(n₁-1)s₁² + (n₂-1)s₂²] / (n₁+n₂-2) | Comparing two sample means with equal variances assumed | Weighted average of two sample variances |
| Variance of Binomial Distribution | σ² = npq | For probability distributions with binary outcomes | Where n=trials, p=success probability, q=(1-p) |
| Variance of Discrete Distribution | σ² = Σ[x²·P(x)] – μ² | For discrete probability distributions | Expected value of squared deviations in probability context |
Detailed Explanations for Students
1. Population vs. Sample Variance
Main Difference: The denominator!
- Population variance uses N (total count)
- Sample variance uses (n-1), called “Bessel’s correction”
Why (n-1)?
When estimating population variance from a sample, dividing by (n-1) instead of n provides an unbiased estimate. This compensates for the sample’s tendency to underestimate population variability.
2. Standard Deviation: The Practical Partner
While variance is in squared units, standard deviation returns to the original units, making it more interpretable:
- If measuring height in centimeters, variance is in cm²
- Standard deviation is in cm (same as original data)
3. Coefficient of Variation: The Comparison Tool
CV allows you to compare variability between datasets with different units or scales:
- Dataset A: Mean = 50, SD = 10 → CV = 20%
- Dataset B: Mean = 500, SD = 50 → CV = 10%
Despite having larger absolute variation, Dataset B is relatively less variable.
4. Sxx in Regression Analysis
Sxx represents the total variation in x-values and is crucial for:
- Calculating correlation coefficients
- Computing regression line slopes
- Determining coefficient of determination (R²)
Step-by-Step Calculation Examples
Example 1: Sample Variance
Data: 5, 8, 10, 12, 15
Step 1: Calculate mean: x̄ = (5+8+10+12+15)/5 = 10
Step 2: Find deviations: -5, -2, 0, 2, 5
Step 3: Square deviations: 25, 4, 0, 4, 25
Step 4: Sum squared deviations: 58
Step 5: Divide by (n-1): s² = 58/4 = 14.5
Example 2: Coefficient of Variation
Mean = 100, Standard Deviation = 15
CV = (15/100) × 100% = 15%
This indicates moderate variability relative to the mean.
Common Student Mistakes to Avoid
- Confusing N and (n-1): Always use (n-1) for sample variance
- Forgetting to square deviations: Must square before summing
- Units confusion: Remember variance is in squared units
- Negative variance: Impossible! Check calculations if this occurs
- Using wrong formula: Match formula to data type (population/sample)
Practical Applications
In Education: Measuring consistency in student performance
In Finance: Assessing investment risk and volatility
In Quality Control: Monitoring manufacturing process consistency
In Research: Analyzing experimental data variability
In Sports: Evaluating athlete performance consistency
Quick Reference Guide
| If you need to… | Use this formula |
|---|---|
| Measure spread in entire population | Population Variance (σ²) |
| Estimate spread from a sample | Sample Variance (s²) |
| Express spread in original units | Standard Deviation (σ or s) |
| Compare different datasets | Coefficient of Variation (CV) |
| Work with frequency tables | Grouped Data Variance |
| Analyze relationships between variables | Sxx Formula |
FAQs on Variance Formula
Q. What is the variance formula in statistics?
Q. What is the formula for variance?
- Population variance: σ² = Σ(x − μ)² / N
- Sample variance: s² = Σ(x − x̄)² / (n − 1)
Q. Why do we divide by (n − 1) in sample variance?
Q. What is the difference between variance and standard deviation?
Q. What is the variance formula for grouped data?
For grouped data, use frequencies:
σ² = Σ f(x − x̄)² / Σ fwhere f is frequency and x is the class midpoint.
Q. How do you calculate variance step by step?
- Find the mean.
- Subtract the mean from each value.
- Square each difference.
- Average the squared differences (divide by N for population, n − 1 for sample).
Q. Can variance be negative?
Q. What is the shortcut formula for variance?
The shortcut (computational) form is:
σ² = (Σx² / N) − μ²It helps reduce arithmetic when datasets are large.
Q. Why is variance important in statistics?
Q. What are real-life applications of variance?
Conclusion
Understanding variance formulas is essential for statistical analysis across all academic disciplines. This comprehensive guide provides the complete toolkit for calculating and interpreting variability in data. Practice with different datasets to build confidence in selecting and applying the appropriate formula for your specific situation.
Remember: Variance quantifies spread, standard deviation makes it interpretable, and the coefficient of variation enables meaningful comparisons. Master these concepts, and you’ll have a solid foundation in statistical analysis.


